A Gentle Introduction to Haskell, version 98

À ce stade nous avons montré comment la correspondance était réalisée sur des motifs individuels, que certains étaient réfutables et d'autres irréfutables, etc. Mais qu'est-ce qui conduit ce processus dans son ensemble? Dans quel ordre les correspondances sont-elles testées? Qu'arrive-t-il si toutes échouent? Cette section aborde ces questions.

La correspondance de motifs peut soit échouer soit réussir ou encore diverger. Une correspondance positive (ou réussie) lie les paramètres formels dans le motif. Une divergence intervient lorsqu'une valeur requise dans le motif contient une erreur ( _|_). Le processus de mise en correspondance se fait de haut en bas et de gauche à droite. Si une correspondance échoue où que ce soit dans une équation, toute l'équation échoue et l'équation suivante est testée. Si toutes les équations échouent, la valeur de l'application de la fonction est _|_, et une erreur à l'exécution en résulte.

Par exemple, si [1,2] est comparé à [0,bot], alors 1 ne correspond pas à 0 et la correspondance échoue. (Rappelez vous que bot, défini précédemment, est une variable liée à _|_). Mais si [1,2] est comparé à [bot,0], alors la comparaison 1 à bot provoque une divergence (c.-à-d. _|_).

L'autre particularité de cet ensemble de règles est que les motifs de niveau supérieur peuvent aussi être accompagnés de gardes booléens, comme dans cette définition d'une fonction qui retourne le signe d'un nombre :

sign x |  x >  0        =   1
       |  x == 0        =   0
       |  x <  0        =  -1

Notez qu'une séquence de gardes peut être fournie pour le même motif. Comme pour les motifs, ils sont évalués de haut en bas et de gauche à droite, et le premier dont l'évaluation retourne True (vrai) aboutit à une correspondance positive.

Les règles de correspondance de motifs peuvent avoir de subtils effets sur la signification d'une fonction. Par exemple, considérons cette définition de take :

take  0     _           =  []
take  _     []          =  []
take  n     (x:xs)      =  x : take (n-1) xs

et cette version légèrement différente (les deux premières équations ont été interverties) :

take1  _     []         =  []
take1  0     _          =  []
take1  n    (x:xs)      =  x : take1 (n-1) xs

Maintenant notez ce qui suit :

take  0   bot  => []
take1 0   bot  =>  Š¥
take  bot []   =>  Š¥
take1 bot []   => []

nous voyons que take est « plus définie » concernant son deuxième argument, alors que take1 est plus définie concernant sont premier argument. Il est difficile de dire, dans ce cas, quelle définition est la meilleure. Rappelez-vous simplement que dans certaines applications, cela peut faire une différence. (Le Prélude Standard inclut une définition correspondante à take).

La correspondance de motifs fournit un moyen de répartir des contrôles basés sur les propriétés structurelles d'une valeur. Dans bien des cas, nous ne souhaitons pas définir une fonction chaque fois qu'une correspondance de motifs est nécessaire, mais à ce stade nous avons uniquement abordé les correspondances de motifs dans la définition des fonctions. Les expressions casuelles dans Haskell permettent de résoudre ce problème. En fait, dans le Haskell Report, la signification des correspondances de motifs dans les définitions de fonctions est spécifiée en termes d'expressions casuelles, qui sont considérées comme étant plus primitives. En particulier, la définition d'une fonction de la forme :

f p11 ... p1k = e1
...
f pn1 ... pnk = en

ou chaque pij est un motif, est sémantiquement équivalente à :

f x1 x2 ... xk = case (x1, ... , xk) of
 (p11, ... ,p1k) -> e1
...
 (pn1, ... ,pnk) -> en

ou les xi sont de nouveaux identificateurs (pour une explication plus générale incluant les gardes, voir §4.4.2). Par exemple, la définition de take donnée plus haut est équivalente à :

take m ys               = case (m,ys) of
                              (0,_)       ->  []
                              (_,[])      ->  []
                              (n,x :xs)   ->  x : take (n-1) xs

Pour être complet à propos des types, un point que nous n'avons pas encore précisé : les types dans le terme droit d'une expression casuelle ou d'un ensemble d'équations comprenant une définition de fonction, doivent tous être les mêmes. Plus précisément, ils doivent tous partager le même type principal commun.

Les règles de correspondance de motifs pour les expressions casuelles sont les mêmes que celles données pour les définitions de fonctions, il n'y a donc rien de nouveau à apprendre ici, si ce n'est de noter le confort offert pas les expressions casuelles. En fait, il y a un usage des expressions casuelles qui est si courant qu'il a sa propre syntaxe : l’« expression conditionnelle ». Dans Haskell, les expressions conditionnelles ont la forme familière :

if e1 then e2 else e3

qui n'est jamais qu'un raccourci pour :

case e1 of True  -> e2
           False -> e3

À partir de là il devrait être clair que e1 doit être de type Bool, et que e2 et e3 doivent être de même type (arbitrairement défini). En d'autres termes, if-then-else vu en tant que fonction est de type Bool->a->a->a.

Il existe un autre type de motif autorisé dans Haskell. Il est nommé motif paresseux, et est de la forme ~pat. Les motifs paresseux sont irréfutables : une correspondance de la valeur v avec ~pat est toujours positive, quel que soit pat. D'un point de vue opérationnel, si un identificateur dans pat devait être « utilisé » plus tard dans le terme droit, il sera lié à la portion de la valeur qui résulterait de la correspondance entre pat et v, et _|_ autrement.

Les motifs paresseux sont utiles dans les contextes ou des structures de données infinies sont définies récursivement. Par exemple, les listes infinies sont un excellent vecteur pour écrire des programmes de simulation, et dans ce contexte les listes infinies sont souvent appelées flux. Considérons le cas simple de la simulation d'une interaction entre un processus serveur server et un processus client client, où client envoie une séquence de requêtes au server, et server répond à chaque requête par une réponse. Cette situation est schématisée dans la figure suivante. (Notez que client accepte un message initial en tant qu'argument).

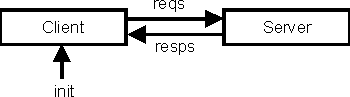
En utilisant des flux pour simuler la séquence de messages, le code Haskell correspondant à ce schéma est :

reqs                     = client init resps
resps                    = server reqs

Ces équations récursives sont une traduction lexicale directe du schéma.

Supposons que la structure du serveur et du client ressemblent à cela :

client init (resp :resps) = init : client (next resp) respsserver      (req :reqs)   = process req : server reqs

où nous supposons que next est une fonction qui, une réponse du serveur ayant été reçue, détermine la requête suivante, et process est une fonction qui traite une requête du client, retournant une réponse appropriée.

Malheureusement, ce programme a un sérieux problème : il ne produira aucune sortie ! Le problème est que le client, tel qu'utilisé dans l'appel récursif de reqs et resps, teste une correspondance sur la liste de réponses avant d'avoir soumis sa première requête! En d'autres termes, la correspondance de motif intervient « trop tôt ». Une manière de résoudre ce problème est de redéfinir client comme suit :

client init resps         = init : client (next (head resps)) (tail resps)

Même si elle fonctionne, cette solution ne se lit pas aussi aisément que la définition précédente. Une meilleure approche consiste à utiliser un motif paresseux :

client init ~(resp :resps) = init : client (next resp) resps

Puisque les motifs paresseux sont irréfutables, la correspondance est immédiatement positive, permettant à la requête initiale d'être « soumise », ce qui, en retour, permet à la première réponse d'être générée. Le moteur est donc « lancé », et la récursion s'occupe du reste.

Pour une démonstration de ce programme en action, si nous définissons :

init                    = 0
next resp               = resp
process req             = req+1

alors nous voyons que :

take 10 reqs => [0,1,2,3,4,5,6,7,8,9]

Pour un autre exemple de l'utilisation des motifs paresseux, considérons la définition de Fibonacci donnée précédemment :

fib             = 1 : 1 : [ a+b | (a,b) <- zip fib (tail fib) ]

Nous pourrions essayer de la réécrire en utilisant un motif nommé :

fib@(1 :tfib)    = 1 : 1 : [ a+b | (a,b) <- zip fib tfib ]

Cette version de fib a le (léger) avantage de ne pas utiliser tail dans le terme droit, puisqu'il est disponible dans une forme « déstructurée » dans le terme gauche en tant que tfib.

[Ce genre d'équation est appelée un motif de liaison (pattern binding) parce que c'est une équation niveau supérieur dans laquelle l'intégralité du terme gauche est un motif, c.-à-d. fib et tfib sont des liens à l'intérieur du cadre de la déclaration.]

En reprenant le même raisonnement que tout à l'heure, nous serions tentés de croire que ce programme ne générera aucune sortie. Et pourtant, il le fait, et la raison en est simple : dans Haskell, les motifs de liaison sont supposés avoir un ~ implicite à leur gauche, reflétant le comportement le plus commun attendu d'un motif de liaison, et évitant des situations anormales qui dépassent le cadre de ce tutoriel. Nous voyons donc que les motifs paresseux jouent un rôle important dans Haskell, ne serait-ce qu'implicitement.

Il est souvent souhaitable de créer un cadre emboîté à l'intérieur d'une expression, dans le but de créer des liens locaux qui ne seront pas visibles ailleurs – c.-à-d. une espèce de forme structurée en blocs. Dans Haskell, il y a deux manières de réaliser cela.

Les expressions Let

Les expressions Let dans Haskell sont utiles chaque fois qu'un lien emboîté est requis. Pour en donner un exemple simple, considérons :

let y   = a*b
    f x = (x+y)/y
in f c + f d

L'ensemble de liaisons créé par une expression let est mutuellement récursif , et les motifs de liaison sont traités comme des motifs paresseux (c.-à-d. qu'ils sont implicitement précédés d'un ~). Les seuls types de déclarations autorisées sont la signature de type, les liaisons de fonctions, et les liaisons de motifs.

Les clauses where

Il est parfois pratique de délimiter les liaisons de plusieurs équations incluant une garde, ce qui nécessite une clause where :

f x y  |  y>z           =  ...
       |  y==z          =  ...
       |  y<z           =  ...
     where z = x*x

Notez que l'on ne peut pas faire cela avec une expression let, qui délimite uniquement l'expression qu'elle renferme. Une clause where n'est autorisée qu'au niveau supérieur d'un ensemble d'équations ou d'une expression casuelle. Les propriétés et contraintes sur les liaisons dans une expression let s'appliquent également à celles dans les clauses where.

Ces deux formes de cadres emboîtés sont très proches, mais rappelez-vous qu'une expression let est une expression, alors qu'une clause where n'en est pas une –elle fait partie de la syntaxe d'une déclaration de fonction ou d'une expression casuelle.

Le lecteur se demande peut-être : comment Haskell évite l'utilisation des points-virgules, ou tout autre délimiteur, pour marquer la fin des équations, déclarations, etc. Par exemple, considérons cette expression let de la section précédente :

let y   = a*b
    f x = (x+y)/y
in f c + f d

Comment l'analyseur syntaxique s'y prend-il pour ne pas interpréter cela comme l'équivalent de :

let y   = a*b f
    x   = (x+y)/y
in f c + f d

?

La réponse est que Haskell utilise une syntaxe à deux dimensions appelée mise en forme (ou layout) qui repose essentiellement sur le fait que les déclarations sont « alignées en colonnes ». Dans l'exemple ci-dessus, notez que y et f commencent à la même colonne. Les règles qui s'appliquent à cette mise en forme sont données en détail dans le Haskell Report (voir §2.7, §B.3), mais en pratique, cette mise en forme est plutôt intuitive. Il faut simplement se rappeler deux choses :

Premièrement, le caractère qui détermine la colonne de départ pour les déclarations dans les clauses where, let, ou les expressions casuelles est celui qui suit immédiatement les mot-clés where, let ou of (cette règle s'applique également à where quand il est utilisé dans une déclaration de classe ou d'instance qui seront introduites dans la section 5). Par conséquent, nous pouvons démarrer la déclaration sur la même ligne que le mot-clé, la ligne suivante, etc. (Le mot-clé do, qui sera abordé plus tard, utilise aussi cette mise en forme).

Deuxièmement, il faut s'assurer que la colonne de départ est décalée à droite par rapport à la colonne de départ associée à la clause qui l'englobe (pour éviter toute ambiguïté). La « fin » d'une déclaration intervient lorsque quelque chose apparaît à la colonne associée avec cette forme de liaison, ou à gauche de celle-ci. Haskell respecte la convention qui veut qu'une tabulation vaille 8 espaces. Il faut donc faire attention avec les éditeurs qui peuvent respecter d'autres conventions.

La mise en forme est en réalité un raccourci pour un mécanisme de groupage explicite, qui mérite d'être mentionné puisqu'il peut être utile dans certaines circonstances. L'exemple let donné plus haut est équivalent à :

let { y   = a*b
  ; f x = (x+y)/y
    }
in f c + f d

Notez les crochets cursifs et le point-virgule explicites. Un cas où cette notation explicite est utile est lorsque l'on souhaite placer plus d'une déclaration sur une ligne. Par exemple, voici une expression valide :

let y   = a*b;  z = a/b
    f x = (x+y)/z
in f c + f d

Pour un autre exemple de délimitation explicite, voir §2.7. L'utilisation de la mise en forme réduit la confusion associée aux listes de déclarations, et améliore donc la lisibilité. Elle est facile à apprendre et son utilisation est encouragée.