III. Les Fonctions▲
Étant donné que Haskell est un langage fonctionnel, on pourrait s'attendre à ce que les fonctions y jouent un rôle majeur…et on aurait raison. Dans cette section, nous abordons différents aspects des fonctions dans Haskell.
Pour commencer, considérons cette définition d'une fonction qui additionne ses deux arguments :
add :: Integer -> Integer -> Integer
add x y = x + yCeci est un exemple de fonction curryfiée. Une application de add est de la forme add e1 e2, et est équivalente à (add e1) e2, puisque les applications des fonctions sont associatives à gauche. En d'autres termes, l'application de la fonction add au premier argument retourne une nouvelle fonction qui est à son tour « appliquée » au deuxième argument. Ceci est conforme au type de add, Integer->Integer->Integer qui est équivalent à Integer->(Integer->Integer). Puisque -> est associatif à droite. Nous pouvons redéfinir différemment la fonction inc (définie au chapitre précédent) en utilisant add :
inc = add 1inc ainsi redéfinie est un exemple d'application partielle d'une fonction curryfiée, et c'est une façon, parmi d'autres, de retourner une fonction en tant que valeur. Considérons un cas ou le passage d'une fonction en tant qu'argument est utile. La fameuse fonction map en est un parfait exemple :
map :: (a->b) -> [a] -> [b]
map f [] = []
map f (x :xs) = f x : map f xsLes applications de fonctions ont la priorité sur n'importe quel opérateur infixe et, par conséquent, le terme droit de la seconde équation est équivalent à (f x) : (map f xs). La fonction map est polymorphe et son type indique clairement que son premier argument est une fonction. Notons également que les occurrences des deux a doivent être de même type (il en est de même pour les b). Pour voir map en action, nous pouvons incrémenter les éléments d'une liste :
map (add 1) [1,2,3] => [2,3,4]Ces exemples démontrent que les fonctions sont bien de « première classe » et elles sont souvent appelées fonctions d'ordre supérieur lorsqu'elles sont utilisées ainsi.
III-A. Les abstractions lambda▲
Plutôt que d'utiliser des équations pour définir les fonctions, nous pouvons aussi les définir « anonymement » via une abstraction lambda. On pourrait, par exemple, définir une fonction équivalente à \x -> x+1. De la même manière, la fonction add est équivalente à \x -> \y -> x+y. Les abstractions lambda emboîtées telles que celle-ci peuvent être écrites en utilisant la notation raccourcie équivalente \x y -> x+y. En réalité, les équations :
inc x = x+1
add x y = x+yne sont que des raccourcis pour :
inc = \x -> x+1
add = \x y -> x+yNous aurons encore à dire sur de telles équivalences plus tard. En général, sachant que x est de type t1 et exp est de type t2, alors \x->exp est de type t1 -> t2.
III-B. Opérateurs infixes▲
Les opérateurs infixes ne sont que des fonctions, et peuvent aussi être définis à l'aide d'équations. Voici, par exemple, la définition d'un opérateur de concaténation de listes.
(++) :: [a] -> [a] -> [a]
[] ++ ys = ys
(x :xs) ++ ys = x : (xs++ys)[D'un point de vue lexical, les opérateurs doivent être des « symboles », contrairement aux identificateurs normaux qui sont alphanumériques ( §2.4). Dans Haskell, il n'y a pas d'opérateurs préfixes, à l'exception du signe moins (-) qui peut aussi bien être infixé que préfixé.]
Un autre exemple est celui du précieux opérateur infixe pour la composition de fonctions :
(.) :: (b->c) -> (a->b) -> (a->c)
f . g = \x -> f (g x)III-B-1. Sections▲
Puisque les opérateurs infixes ne sont que des fonctions, il est logique qu'ils puissent aussi être utilisés dans des applications partielles. Dans Haskell, une application partielle sur un opérateur infixe est appelée une section. Par exemple :
(x+) = \y -> x + y
(+y) = \x -> x + y
(+) = \x y -> x + y[Les parenthèses sont obligatoires.]
La dernière forme de section donnée ci-dessus astreint un opérateur infixe à une valeur de fonction équivalente, ce qui est pratique lorsque l'on doit passer un opérateur infixe en tant qu'argument à une fonction, par exemple dans map (+) [1,2,3] (le lecteur devrait s'assurer, par lui-même, que ceci retourne bien une liste de fonctions !). Cela est également nécessaire lorsque l'on définit la signature de type d'une fonction, comme dans les exemples de (++) et de (.) donnés précédemment.
Nous pouvons maintenant voir que add défini précédemment n'est que (+), et inc n'est que (+1) ! En fait, les définitions suivantes feraient aussi bien l'affaire :
inc = (+ 1)
add = (+)Nous pouvons astreindre des opérateurs infixes à prendre une valeur de fonction équivalente, mais l'opération inverse est-elle possible ? Oui ! Il suffit de mettre l'identificateur lié à une valeur de fonction entre guillemets inversés. Par exemple, x `add ` y est l'équivalent de add x y.
Certaines fonctions se comprennent mieux de cette manière. Un bon exemple en est le prédicat prédéfini d'appartenance à une liste elem ; L'expression x `elem ` xs peut intuitivement se lire « x est un élément appartenant à xs ».
[Il existe quelques règles particulières concernant les sections incluant l'opérateur préfixe/infixe - ]
À ce stade, le lecteur pourrait être un peu perdu par les innombrables façons de définir une fonction ! La décision de fournir ces mécanismes est due en partie à des conventions historiques, et reflète en partie un désir de cohérence (par exemple, dans le traitement accordé aux infixes « contre » les fonctions).
III-B-2. Les déclarations de fixité▲
Une déclaration de fixité peut être déclarée pour n'importe quel opérateur infixe ou constructeur (y compris ceux faits d'identificateurs ordinaires, tels que `elem `). Cette déclaration permet de spécifier un niveau de priorité allant de 0 à 9 (9 étant le plus élevé. Le niveau de priorité supposé d'une application normale étant 10), ainsi que left- (gauche), right- (droite), ou non-associativité. Par exemple, les déclarations de fixité de ++ et . sont :
infixr 5 ++
infixr 9 .Ces deux exemples spécifient une associativité à droite, la première avec un niveau de priorité 5 et la dernière un niveau 9. L'associativité à gauche se spécifie via infixl, et la non-associativité via infix. En outre, il est possible de spécifier la fixité de plusieurs opérateurs dans la même déclaration. Si aucune déclaration de fixité n'est donnée pour un opérateur particulier, la fixité par défaut infixl 9 sera attribuée. (Voir §5.9 pour une définition détaillée des règles d'associativité).
III-C. Les fonctions sont non-strictes▲
Supposons que bot est définie par :
bot = botEn d'autres termes, bot est une expression sans fin ou non finie. La valeur de telles expressions est abstraitement dénotée par la valeur _|_ (lire « bottom » qui signifie « fond » en anglais). Cette valeur est également attribuée aux expressions dont le résultat aboutit à une erreur d'exécution, telle que 1/0. Une telle erreur est irrécupérable : les programmes ne peuvent pas continuer après ces erreurs. Les erreurs rencontrées par le système d'entrées/sorties, telles qu'une erreur de fin de fichier, sont récupérables et sont traitées différemment. (De telles erreurs d'entrées/sorties ne sont pas réellement des erreurs, mais plutôt des exceptions. Les exceptions seront traitées en détail dans la section 7).
Une fonction f est dite stricte si, lorsqu'elle est appliquée à une expression non finie, elle ne se termine pas non plus. En d'autres termes, f est stricte ssi (si et seulement si) la valeur de f bot est _|_. Dans la plupart des langages de programmation, toutes les fonctions sont strictes. Mais ce n'est pas le cas dans Haskell. Considérons, pour l'exemple, const1, la fonction constante 1, définie par :
const1 x = 1Dans Haskell, la valeur de const1 bot est 1. D'un point de vue opérationnel, puisque const1 n'a pas « besoin » de la valeur de son argument, celui-ci n'est jamais évalué et, par conséquent, const1 ne provoque jamais de calcul sans fin. Pour cette raison, les fonctions non strictes sont également appelées des « fonctions paresseuses », et on dit qu'elles évaluent leurs arguments avec « paresse », ou « à la demande » (en anglais on parle de « lazy evaluation »).
Le paragraphe ci-dessus vaut aussi pour les erreurs, puisque les erreurs et les valeurs non finies sont sémantiquement identiques pour Haskell. Par exemple, l'évaluation de const1 (1/0) retourne correctement 1.
Les fonctions non strictes sont extrêmement utiles dans plusieurs contextes. L'avantage principal est qu'elles libèrent le programmeur de beaucoup de soucis concernant l'ordre des évaluations. Des valeurs qui exigent un calcul lourd peuvent être passées à des fonctions sans craindre qu'elles soient calculées si cela n'est pas nécessaire. Un exemple significatif est celui d'une structure de données qui peut être infinie.
Abordons les fonctions non strictes sous un autre angle : les calculs opérés par Haskell se basent sur des « définitions » plutôt que sur les « assignations » utilisées dans les langages traditionnels. Une déclaration telle que :
v = 1/0se lit : « définir v comme étant 1/0 », mais ne se lit pas : « calculer 1/0 et stocker le résultat dans v ». C'est uniquement quand la valeur (définition) de v sera nécessaire que la division par zéro se produira. Par elle même, cette déclaration n'implique aucun calcul. La programmation par assignations requiert une grande attention dans l'ordre des assignations : la signification d'un programme dépend de l'ordre dans lequel ces assignations sont exécutées. À l'inverse, les définitions sont beaucoup plus simples : elles peuvent être présentées dans n'importe quel ordre sans affecter la signification d'un programme.
III-D. Les structures de données « infinies »▲
Un des avantages de la nature non stricte de Haskell est que les constructeurs de données sont également non-stricts. Ce n'est pas surprenant, puisque les constructeurs ne sont jamais que des fonctions d'un certain type (ils ne se distinguent des fonctions que parce qu'ils peuvent être utilisés pour une correspondance de motif). Par exemple, le constructeur de listes, (:), est non strict.
Les constructeurs non stricts permettent la définition de structures de données (conceptuellement) infinies. Voici une liste infinie de uns :
uns = 1 : unsLa fonction numsFrom est peut-être encore plus intéressante :
numsFrom n = n : numsFrom (n+1)Donc numsFrom n est la liste infinie des entiers successifs à partir de n. Nous pouvons créer une liste infinie de carrés à partir de numsFrom :
squares = map (^2) (numsFrom 0)(Notez l'utilisation d'une section ; ^ étant l'opérateur infixe d'exponentiation.)
Bien entendu, nous souhaitons éventuellement extraire une portion finie de cette liste pour un calcul et il existe un grand nombre de fonctions dans Haskell qui font ce genre de choses : take, takewhile, filter pour ne citer qu'elles. Les définitions de Haskell incluent un large ensemble de fonctions et de types internes – cela se nomme le « Prélude Standard ». Le Prélude Standard complet est inclus dans la section 8 de la première partie du Haskell report. Voir la partie nommée PreludeList pour les fonctions opérant sur des listes. Par exemple, take retourne les n premiers éléments d'une liste :
take 5 squares => [0,1,4,9,16]La définition de uns ci-dessus est un exemple de liste circulaire. Dans la plupart des circonstances, la paresse a un impact important sur l'efficacité, puisqu'on peut attendre d'une implémentation qu'elle implémente cette liste comme une réelle structure circulaire, économisant ainsi la mémoire.
Un autre exemple de l'utilisation de la circularité est la suite de Fibonacci qui peut être calculée efficacement avec la suite infinie suivante :
fib = 1 : 1 : [ a+b | (a,b) <- zip fib (tail fib) ]ou zip est une fonction du Prélude Standard qui retourne une liste de paires composées des éléments de même position dans les deux listes.
zip (x :xs) (y :ys) = (x,y) : zip xs ys
zip xs ys = []Remarquez de quelle manière fib, une liste infinie, est définie en fonction d'elle même, comme si elle courrait après sa propre queue. Un schéma de ce calcul figure sous 1.
Pour une autre définition de liste infinie, voir section 4.4
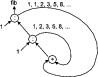
III-E. La fonction d’erreur▲
Haskell a une fonction interne appelée error dont le type est String->a. C'est une fonction un peu étrange : à en juger par son type, il semble qu'elle retourne la valeur d'un type polymorphe à propos duquel elle ne sait rien, puisqu'à aucun moment un argument de ce type ne lui est passé.
En fait, il y a une valeur « partagée » par tous les types : Š¥. En effet, c'est cette valeur qui est systématiquement retournée par une erreur (rappelez-vous que les erreurs ont la valeur _|_). Cependant, nous pouvons attendre d'une implémentation raisonnable qu'elle envoie l'argument String à error à des fins de diagnostic. Cette fonction est donc utile lorsque nous voulons qu'un programme se termine si quelque chose a « mal tourné ». Par exemple, la définition réelle de head du Prélude Standard est :
head (x :xs) = x
head [] = error "head{PreludeList} : head []"

